Basics

In this example we will demonstrate the use of FMMAX for a basic diffraction calculation.

Preliminaries

The first step of a simulation is to specify the unit cell by defining the primitive lattice vectors. In this case, we will use a simple square unit cell with basis vectors \(\mathbf{u}=\hat{\mathbf{x}}=(1, 0)\) and \(\mathbf{v}=\hat{\mathbf{y}}=(0, 1)\).

import fmmax

primitive_lattice_vectors = fmmax.LatticeVectors(u=fmmax.X, v=fmmax.Y)

In the Fourier modal method, the magnetic fields in the unit cell are given by,

\[ \mathbf{H}(\mathbf{r}, z) = \sum_{l=0}^{N-1} \mathbf{H}_l(z) e^{i(\mathbf{k} + \mathbf{G}_l)\cdot \mathbf{r}} \]

where \(\mathbf{G}_l\) are the reciprocal lattice vectors and \(\mathbf{k}\) is the in-plane wavevector for the excitation.

The set of reciprocal lattice vectors are define the expansion; when generating an expansion, we only specify the approximate number of terms; the actual number may differ. This is done to ensure that the expansion is always symmetric, i.e. if a particular \((k_{x}, k_{y})\) term is included, then all of \((\pm k_{x}, \pm k_{y})\) are included. In FMMAX, the vectors \(\mathbf{G}_l\) are ordered by magnitude, so that \(\mathbf{G}_0 = \mathbf{0}\).

expansion = fmmax.generate_expansion(primitive_lattice_vectors, approximate_num_terms=120)
n = expansion.num_terms
print(f"Actual number of terms in expansion: {n}")

Actual number of terms in expansion: 121

The expansion contains a basis_coefficients attribute which gives the Fourier order associated with each \(\mathbf{G}_l\). We’ll take a look at the first few order in our expansion.

expansion.basis_coefficients.tolist()[:5]

[[0, 0], [-1, 0], [0, -1], [0, 1], [1, 0]]

As expected, the first term corresponds to the (0, 0), order.

The in-plane wavevector is associated with the excitation, and for plane waves is chosen so that the zeroth order corresponds propagation in a target direction, i.e. specific polar and azimuthal angles. The in-plane wavevector depends upon these angles as well as the wavelength and the permittivity of the medium in which light propagates in the target direction. Here, we’ll consider a plane wave in vacuum with 0.65 μm wavelength that is incident at 30 degrees.

import jax.numpy as jnp

wavelength = jnp.asarray(0.65)
in_plane_wavevector = fmmax.plane_wave_in_plane_wavevector(
    wavelength=wavelength,
    polar_angle=jnp.deg2rad(30.0),
    azimuthal_angle=jnp.asarray(0.0),
    permittivity=jnp.asarray(1.0),
)

Structure definition

Next, we’ll define the structure. The structure consists of layers, and for each we need an array defining the permittivity and a scalar thickness.

Permittivity arrays must be at least two-dimensional, with the two trailing axes corresponding to the \(u\) and \(v\) directions (\(x\) and \(y\) in this case). In the case of uniform layers (i.e. layers in which the permittivity does not vary spatially), it is best for the trailing axes to have shape (1, 1). This triggers a special code path which computes layer eigenmodes analytically, which is more efficient and generally more accurate.

Here, we’ll model a rectangular pillar comprised of \(n=1.85\) media on a \(n=1.45\) substrate.

permittivity_ambient = jnp.asarray([[1.0 + 0.0j]])**2
permittivity_substrate = jnp.asarray([[1.45 + 0.0j]])**2
print(f"Permittivity shape for uniform layers: {permittivity_ambient.shape}")

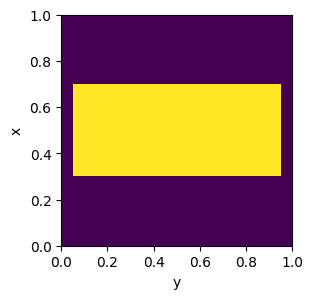
x, y = fmmax.unit_cell_coordinates(primitive_lattice_vectors, shape=(100, 100))
mask = (x > 0.3) & (x < 0.7) & (y > 0.05) & (y < 0.95)
permittivity_pillar = jnp.where(mask, (1.45 + 0.0j)**2, (1.0 + 0.0j)**2)
print(f"Permittivity shape for patterned layer: {permittivity_pillar.shape}")

Permittivity shape for uniform layers: (1, 1)

Permittivity shape for patterned layer: (100, 100)

Let’s visualize the pillar layer permittivity. Note that by FMMAX convention, spatial axes are always ordered as \((x, y, z)\), and hence we swap the \(x\) and \(y\) axes when plotting.

import matplotlib.pyplot as plt

plt.figure(figsize=(3, 3))
ax = plt.subplot(111)
ax.pcolormesh(y, x, permittivity_pillar.real)
ax.set_aspect("equal")
ax.set_xlabel("y")
_ = ax.set_ylabel("x")

Define the thickness for each layer. In the Fourier modal method, the first and last layers effectively extend to infinity. Therefore, their thickness value is essentially arbitrary, and only affects the locations at which amplitudes in the first and last layers are reported.

thickness_ambient = 0.0
thickness_pillar = 0.8
thickness_substrate = 0.0

Calculation of diffraction efficiency

We can now solve for the eigenmodes of each layer, and construct the scattering matrix that relates eigenmode amplitudes at the start and end of our layer stack.

import functools

eigensolve = functools.partial(
    fmmax.eigensolve_isotropic_media,
    wavelength=wavelength,
    in_plane_wavevector=in_plane_wavevector,
    primitive_lattice_vectors=primitive_lattice_vectors,
    expansion=expansion,
)

result_ambient = eigensolve(permittivity=permittivity_ambient)
result_pillar = eigensolve(permittivity=permittivity_pillar)
result_substrate = eigensolve(permittivity=permittivity_substrate)

s_matrix = fmmax.stack_s_matrix(
    layer_solve_results=[result_ambient, result_pillar, result_substrate],
    layer_thicknesses=[thickness_ambient, thickness_pillar, thickness_substrate],
)

The scattering matrix has four blocks, (s11, s12, s21, s22), which relate the forward-going and backward-going eigenmode amplitudes on the two sides of our stack.

a_substrate = s11 @ a_ambient + s12 @ b_substrate
b_ambient = s21 @ a_ambient + s22 @ b_substrate

Here,

• a_ambient is the forward-going light in the ambient, i.e. incident upon the pillar layer.

• a_substrate is forward-going light in the substrate, i.e. light that has transmitted from the ambient through the pillar layer and into the substrate.

• b_ambient is backward-going light in the ambient, reflected from the pillar layer.

• b_substrate is backward-going light in the substrate incident upon the pillar layer.

Each amplitude is a column vector of length 2 * n, with the factor of 2 due to the two possible polarizations for each plane wave in the expansion. In the amplitude vectors, the first n terms correspond to \(x\)-polarized magnetic fields, and the remaining terms are for \(y\)-polarized magnetic fields.

Next, we need to define the incident amplitudes. Since there is no light incident from the substrate, b_substrate is just zeros. Meanwhile, a_ambient is a one-hot vector, with the single nonzero element being the one corresponding to the zeroth order and desired polarization. For \(x\)- and \(y\)-polarized magnetic fields, this is at 0 and n, respectively. We’ll choose the x-polarized field.

b_substrate = jnp.zeros((2 * n, 1), dtype=complex)
a_ambient = jnp.zeros((2 * n, 1), dtype=complex).at[0, 0].set(1)

Now, normalize the excitation so the incident power is unity.

incident, _ = fmmax.amplitude_poynting_flux(
    forward_amplitude=a_ambient,
    backward_amplitude=jnp.zeros_like(a_ambient),
    layer_solve_result=result_ambient,
)
a_ambient /= jnp.sqrt(jnp.sum(incident, axis=-2, keepdims=True))

Now, we can calculate the transmitted and reflected amplitudes.

a_substrate = s_matrix.s11 @ a_ambient
b_ambient = s_matrix.s21 @ a_ambient

Now compute and visualize the transmitted and reflected power into each order. Note that reflected flux is negative, since power flows in the \(-z\) direction.

incident, reflected = fmmax.amplitude_poynting_flux(
    forward_amplitude=a_ambient,
    backward_amplitude=b_ambient,
    layer_solve_result=result_ambient,
)
transmitted, _ = fmmax.amplitude_poynting_flux(
    forward_amplitude=a_substrate,
    backward_amplitude=jnp.zeros_like(a_substrate),
    layer_solve_result=result_substrate,
)

# Sum over the two polarizations.
incident = incident[..., :n, :] + incident[..., n:, :]
reflected = reflected[..., :n, :] + reflected[..., n:, :]
transmitted = transmitted[..., :n, :] + transmitted[..., n:, :]

plt.figure(figsize=(8, 3))
ax = plt.subplot(121)
im = ax.scatter(
    x=expansion.basis_coefficients[:, 1],
    y=expansion.basis_coefficients[:, 0],
    c=transmitted,
    s=100,
    marker="s",
)
ax.set_title("transmitted")
ax.set_xlabel("Diffraction order y")
ax.set_ylabel("Diffraction order x")
ax.set_aspect("equal")
plt.colorbar(im)

ax = plt.subplot(122)
im = ax.scatter(
    x=expansion.basis_coefficients[:, 1],
    y=expansion.basis_coefficients[:, 0],
    c=-reflected,
    s=100,
    marker="s",
)
ax.set_title("$-$reflected")
ax.set_xlabel("Diffraction order y")
ax.set_ylabel("Diffraction order x")
ax.set_aspect("equal")
_ = plt.colorbar(im)

As we can see, most of power is transmitted into the (-1, 0) order. Finally, let’s check to make sure energy is conserved.

print(f"incident = {jnp.sum(incident, axis=-2)}")
print(f"transmitted - reflected = {jnp.sum(transmitted, axis=-2) - jnp.sum(reflected, axis=-2)}")

incident = [0.99999994]
transmitted - reflected = [0.9995693]